In the realms of Data Science you’ll encounter sooner or the later the terms “Precision” and “Recall”. But what do they mean?

Table of Contents
Clarification
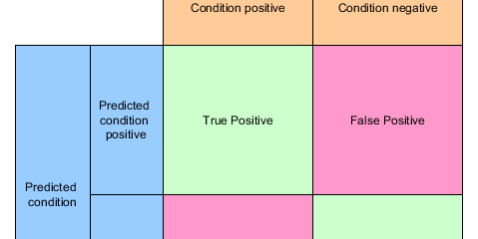
Living together with little kids You very often run into classification issues:
My daughter really likes dogs, so seeing a dog is something positive. When she sees a normal dog e.g. a Labrador and proclaims: “Look, there is a dog!”
That’s a True Positive (TP)
If she now sees a fat cat and proclaims: “Look at the dog!” we call it a False Positive (FP), because her assumption of a positive outcome (a dog!) was false. A false positive is also called a Type 1 error
If I point at a small dog e.g. a Chihuahua and say “Look at the dog!” and she cries: “This is not a dog!” but indeed it is one, we call that a False negatives (FN) A false negativeis also called a Type 2 error
And last but not least, if I show her a bird and we agree on the bird not being a dog we have a True Negative (TN)
This neat little matrix shows all of them in context:
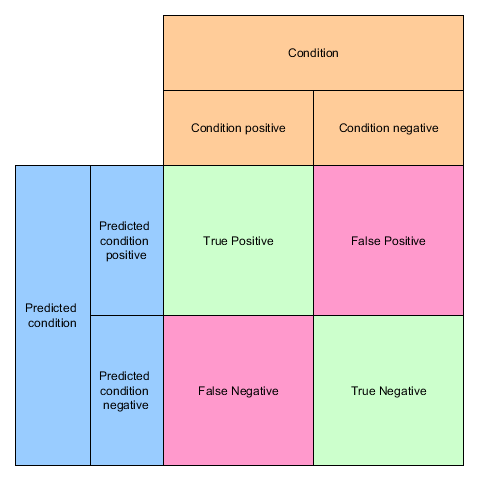
Precision and Recall
If I show my daughter twenty pictures of cats and dogs (8 cat pictures and 12 dog pictures) and she identifies 10 as dogs but out of ten dogs there are actually 2 cats her precision is 8 / (8+2) = 4/5 or 80%.
Precision = TP / (TP + FP)
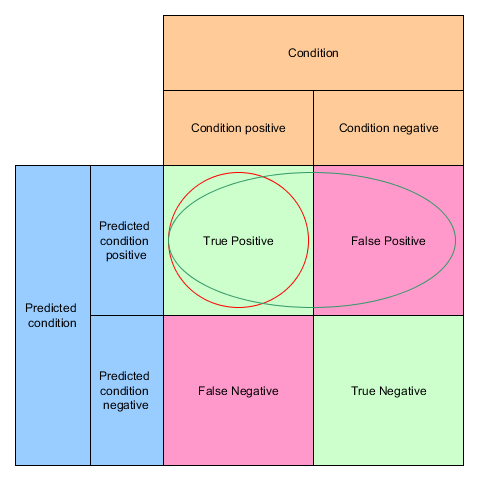
Knowing that there are actually 12 dog pictures and she misses 4 (false negatives) her recall is 8 / (8+4) = 2/3 or roughly 67%
Recall = TP / (TP + FN)

Which measure is more important?
It depends:
If you’re a dog lover it is better to have a high precision, when you are afraid of dogs say to avoid dogs, a higher recall is better 🙂
Different terms
Precision is also called Positive Predictive Value (PPV)
Recall often is also called
- True positive rate
- Sensitivity
- Probability of detection
Other interesting measures
Accuracy
ACC = (TP + TN) / (TP + FP + TN + FN)
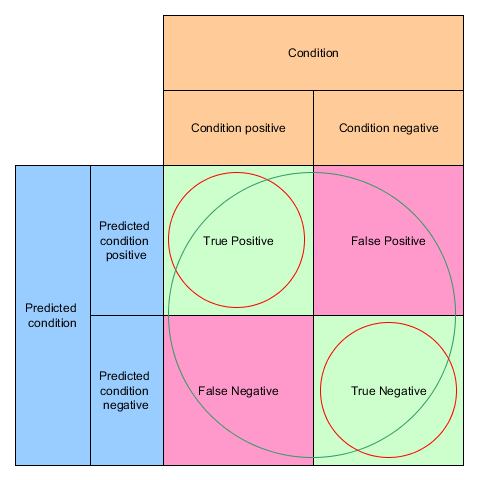
F1-Score
You can combine Precision and Recall to a measure called F1-Score. It is the harmonic mean of precision and recall
F1 = 2 / (1/Precision + 1/Recall)
Scikit-Learn
scikit-learn being a one-stop-shop for data scientists does of course offer functions for calculating precision and recall:
from sklearn.metrics import precision_score y_true = ["dog", "dog", "not-a-dog", "not-a-dog", "dog", "dog"] y_pred = ["dog", "not-a-dog", "dog", "not-a-dog", "dog", "not-a-dog"] print(precision_score(y_true, y_predicted , pos_label="dog"))
Let’s assume we trained a binary classifier which can tell us “dog” or “not-a-dog”
In this example the precision is 0.666 or ~67% because in two third of the cases the algorithm was right when it predicted a dog
from sklearn.metrics import recall_score print(recall_score(y_true, y_pred, pos_label="dog"))
The recall was just 0.5 or 50% because out of 4 dogs it just identified 2 correctly as dogs.
from sklearn.metrics import accuracy_score print(accuracy_score(y_true, y_pred))
The accuracy was also just 50% because out of 6 items it made only 3 correct predictions.
from sklearn.metrics import f1_score print(f1_score(y_true, y_pred, pos_label="dog"))
The F1 score is 0.57 – just between 0.5 and 0.666.
What other scores do you encounter? – stay tuned for the next episode 🙂