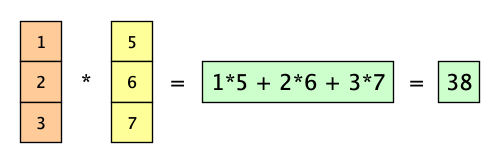Einführung in numpy

Motivation

numpy is das Arbeitspferd für Data Scientists und Machine Learning Engineers. Aber auch als Robotiker kann diese Bibliothek nützlich sein, wenn man zum Beispiel Bildverarbeitung macht.

Es ist eine Bibliothek für numerische Berechnungen und bietet viele Funktionen, die das Arbeiten mit Zahlen erleichtern.
numpy ist schneller als Python-Listen, weil es in C geschrieben ist. Es ist auch effizienter, weil es homogene Datenstrukturen verwendet.
Das bedeutet, dass alle Elemente in einem numpy-Array den gleichen Datentyp haben. numpy ist auch effizienter, weil es Vektorisierung verwendet.
Das bedeutet, dass Operationen auf numpy-Arrays auf einmal auf alle Elemente angewendet werden können, anstatt sie einzeln zu durchlaufen.
Das macht numpy ideal für mathematische Operationen, lineare Algebra, Statistik und maschinelles Lernen.

Historie

numpy wurde 2005 von Travis Oliphant entwickelt. (Damals noch unter dem Namen Numeric.)
Es wurde später in numpy umbenannt, um Verwechslungen mit einem anderen Paket zu vermeiden.
numpy ist Teil des SciPy-Stacks, einer Sammlung von Open-Source-Software für wissenschaftliches Rechnen in Python.
Der SciPy-Stack enthält auch Bibliotheken wie pandas, matplotlib und scikit-learn.

Installation

pip install numpy

Import

import numpy as np

Der `as`-Befehl definiert einen sogenannten Alias. Jetzt können Strukturen aus numpy via np referenziert werden.

ndarray

ndarray ist die wichtigste Datenstruktur in numpy. Sie steht für n-dimensionale Arrays.
Ein Array kann mit der Methode `array` aus einer Liste erstellt werden.

a = np.array([1, 2, 3])
a
array([1, 2, 3])

Ein Array kann auch wieder in eine Liste umgewandelt werden.

b = a.tolist()
b
[1, 2, 3]

Datentypen

Im Gegensatz zu Python-Listen sind numpy-Arrays homogen, d.h. alle Elemente haben den gleichen Datentyp.
Der Datentyp eines Arrays kann mit der Methode `dtype` abgefragt werden.

a.dtype
dtype('int64')

Wenn man ein Array mit einem anderen Datentyp erstellen möchte, kann man explizit den Datentyp angeben.

b = np.array([1, 2, 3], dtype='float')
b
array([1., 2., 3., 4.], dtype=float32)

Vektoren

Wir schauen uns zuerst die Vektorarithmetik an:

Addition / Subtraktion

a = np.array([1, 2, 3])
b = np.array([5, 6, 7])
a + b

Hier werden die Elemente der Arrays elementweise addiert.
das ergibt array([6, 8, 10])

Skalarmultiplikation

a = np.array([1, 2, 3])
3 * a

Hier werden die Elemente des Arrays mit 3 multipliziert.

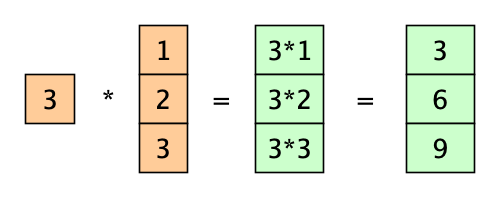
Hier können wir sehen, warum es charmant ist, numpy’s Array für diese Operation zu verwenden.
Wenn wir das mit einer List comprehension machen, sieht das so aus:

c = [1, 2, 3]
d = [x * 3 for x in c]

Das ist weniger intuitiv und auch langsamer.

Skalarprodukt

a = np.array([1, 2, 3])
b = np.array([5, 6, 7])
a.dot(b)

Hier wird das Skalarprodukt berechnet, in dem alle Elemente miteinander multipliziert und dann summiert werden.
Das ergibt in diesem Fall 38.

Hadamard-Produkt

a = np.array([1, 2, 3])
b = np.array([5, 6, 7])
a * b

Hier wird das Hadamard-Produkt berechnet, in dem die Elemente der Arrays elementweise multipliziert werden.
Das ergibt

array([5, 12, 21])

Kreuzprodukt

a = np.array([1, 2, 3])
b = np.array([5, 6, 7])
np.cross(a, b)

Hier wird das Kreuzprodukt berechnet.
Das Ergebnis ist ein neues Array, das das Kreuzprodukt von a und b darstellt.

Matrizen

ndarray kann auch für Matrizen verwendet werden.

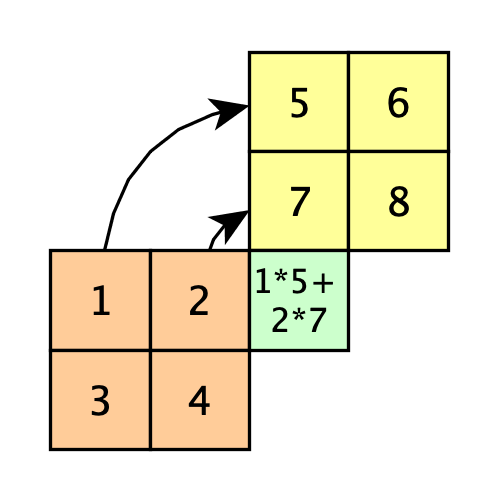
Matrixmultiplikation

Bei der Matrixmultiplikation ist es wichtig, dass die Anzahl der Spalten der ersten Matrix gleich der Anzahl der Zeilen der zweiten Matrix ist.
Dann kann nach dem Schema “Zeile mal Spalte” multipliziert werden. Das kenne wir noch aus der Schulzeit.
Dort haben wir es unter dem Namen Schema von Falk kennengelernt.

a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
a.dot(b)

Hier wird die Matrixmultiplikation durchgeführt.
Das Ergebnis ist ein neues Array, das die Matrixmultiplikation von a und b darstellt.

matmul() und dot() sind äquivalent, aber matmul() sollte bevorzugt werden, weil es klarer ist. Besser noch ist die @-Operator-Syntax.

np.matmul(a, b)
a @ b

Reshape

Mit der Methode reshape kann ein Array in eine andere Form gebracht werden.

a = np.array([1,2,3,4,5,6,7,8])
reshaped = a.reshape([2, 4])
reshaped
array([[1, 2, 3, 4],
[5, 6, 7, 8]])

einsum

einsum ist eine Funktion, die es ermöglicht, die Summation über die Elemente eines Arrays zu steuern.

a = np.array([[1, 2], [3, 4]])
np.einsum('ii', a)

Hier wird die Summe der Diagonalelemente berechnet.
Das Ergebnis ist 5.

ranges und linspace

numpy hat auch Funktionen, um die Erstellung von Arrays zu erleichtern.

arange

arange erstellt ein Array mit einer Sequenz von Zahlen.

a = np.arange(10)
a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

wie die range-Funktion in Python, kann auch arange mit einem Startwert, einem Endwert und einem Schritt verwendet werden.

b = np.arange(1, 10, 2)
b
array([1, 3, 5, 7, 9])

linspace

linspace erstellt ein Array mit einer Sequenz von Zahlen, die gleichmäßig verteilt sind.

a = np.linspace(0, 1, 5)
a
array([0. , 0.25, 0.5 , 0.75, 1. ])

Zufallszahlen

numpy hat auch Funktionen, um Zufallszahlen zu generieren.

rand

rand erstellt ein Array mit Zufallszahlen zwischen 0 und 1.

a = np.random.rand(3)
a
array([0.5488135 , 0.71518937, 0.60276338])

randint

randint erstellt ein Array mit Zufallszahlen zwischen einem Startwert und einem Endwert.

a = np.random.randint(1, 10, 3)
a
array([6, 1, 1])

Fazit

NumPy ist eine leistungsstarke Bibliothek für numerische Berechnungen in Python.
Es bietet viele Funktionen, die das Arbeiten mit Vektoren und Matrizen erleichtern.